武汉菲恩生物科技有限公司品牌商

10 年

手机商铺

商家活跃：

产品热度：

搜本店搜全站

武汉菲恩生物科技有限公司
>公司新闻
>
ELISA标曲拟合方程解析

品牌商

武汉菲恩生物科技有限公司

入驻年限：10 年

联系人：
王经理
所在地区：
湖北武汉市洪山区
业务范围：
ELISA 试剂盒、抗体、试剂、技术服务
经营模式：
生产厂商

在线沟通

电话 QQ 联系

ELISA标曲拟合方程解析

5052 人阅读发布时间：2021-03-09 10:55

ELISA 标准曲线那么多的曲线计算公式，那么对于那么多的曲线计算公式，我该如何选择最佳的拟合方程呢？样本浓度的分析是根据标准品数据所生成的标准曲线完成的，要确保样本结果的准确性，就要保证标准曲线尽量能还原抗原抗体的动力学反应过程。

一般情况按照说明书推荐方法拟合标曲，可以用软件绘制也可以手动制作。标曲呈现s型曲线，两端趋于水平，中间趋于线性，中间部分为较佳的检测范围。当标准品的量超过与包被抗体结合的量，此时标准品已饱和，在增加标准品的量，其 OD 值不再变化，故当标准品达到一定浓度后，曲线趋于水平。按照科学分析方法，如果存在奇异点或者污点，直接采用线性分析不是很好，要对拟合曲线的几个点进行取舍，同时也可以改用双对数直线拟合或者四参数曲线拟合。那么常用的曲线拟合回归方程主要为以下7种：

01 直线回归

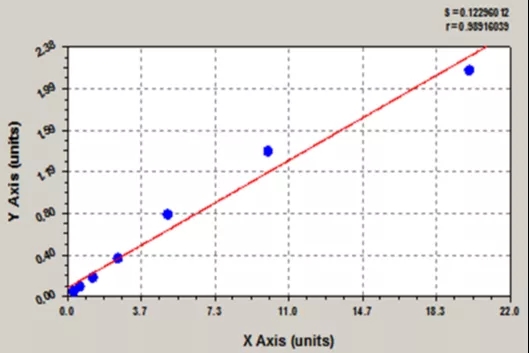
直线回归是最简单的回归模型,也是最基本的曲线拟合回归分析方法，将所有的测试点拟合为一条直线。其拟合函数方程式为：y=a+bx

新闻图片1

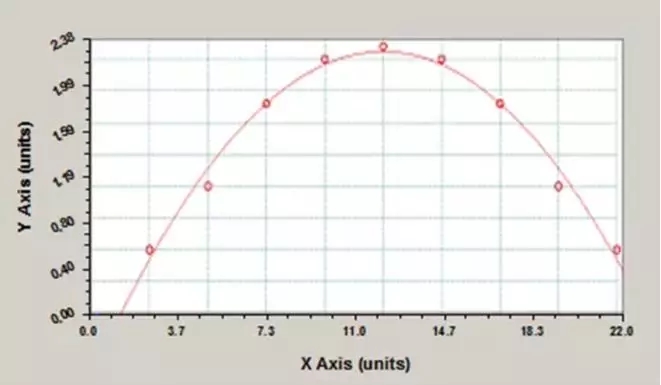
02 二次多项式拟合回归方程

二次多项式成抛物线状，开口向下或者向上，在很多 ELISA 实验中，拟合近似于二次多项式的升段或者降段，由于曲线的特性，同一个浓度值在曲线图上可能表现出没有对应的OD值、有一个 OD 值，或者两个 OD 值，所以使用二次多项式拟合时，最好保证取值的范围都落在曲线的升段或者降段，否则哪怕是相关系数很好也很可能与实际的值不一致。其拟合函数方程式为：y = a + b x + c x2

新闻图片2

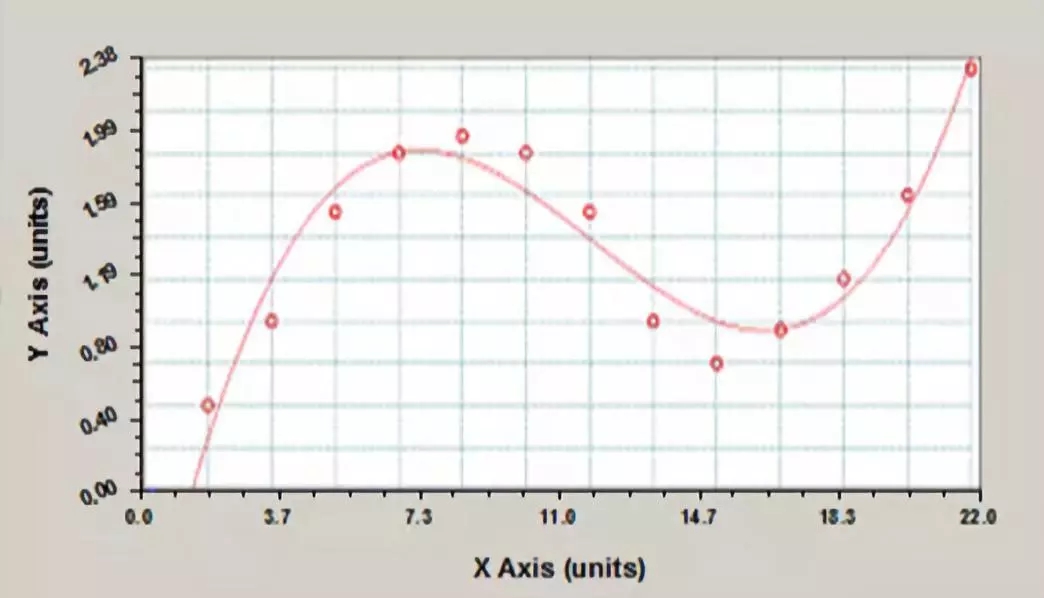
03 三次多项式拟合回归方程

三次多项式像倒状的‘S’形，在实验结果刚好在曲线的升段或者降段的时候，效果还可以，但是对于区间较广的情形, 由于其弯曲的波动，三次方程拟合模拟不一定很好.跟二次方程拟合一样，看曲线的相关系数的同时也要看计算的点在曲线上的分布，这样才算出理想的结果，本软件计算值时，选择性的取相对于浓度或者 OD 值，比较符合实际的那个结果，而没有将多个结果列出。拟合函数方程式为：y = a + b x + c x2 + d x3

新闻图片3

04 半对数拟合回归方程

半对数拟合即将浓度值取对数值，然后再和对应的 OD 值进行直线回归，理想的状态下，在半对数坐标中是一条直线，常用于浓度随着 OD 值的增加或者减低呈对数增加或者减少的情况，即浓度的变化比 OD 值的变化更为剧烈。在 ELISA 实验中较常用（有很多用 EXCEL 画图时，也常使用半对数）。拟合函数方程式为：y = a lg(x) + b

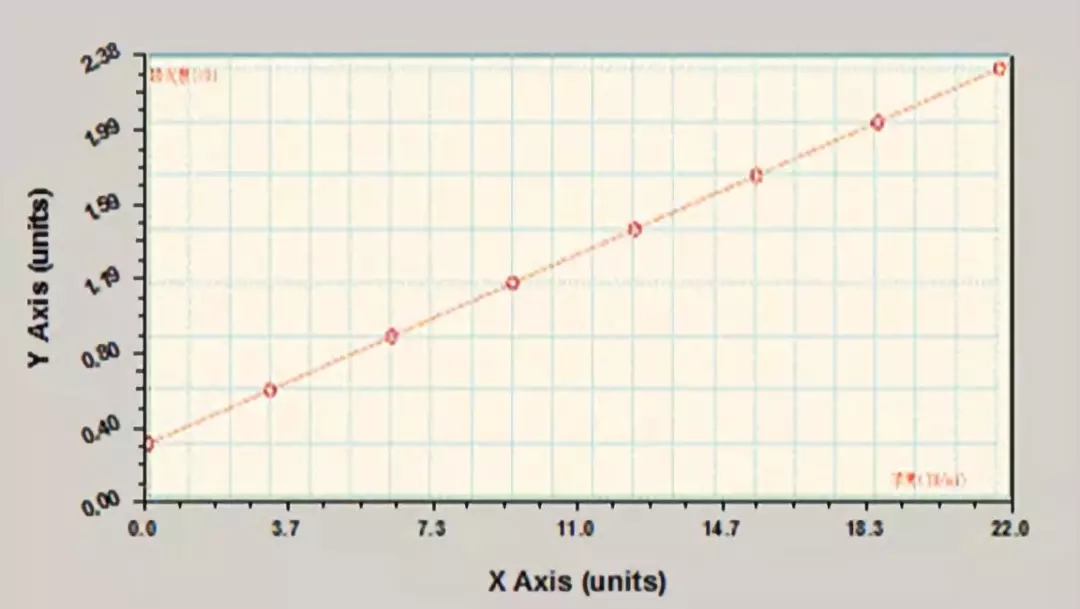
新闻图片4

05 Log-Log 拟合回归方程

Log-Log 拟合和半对数相似,只是将 OD 值和对应的浓度值均取对数，然后再进行直线回归。拟合函数方程式为：lg(y) = a lg(x) + b

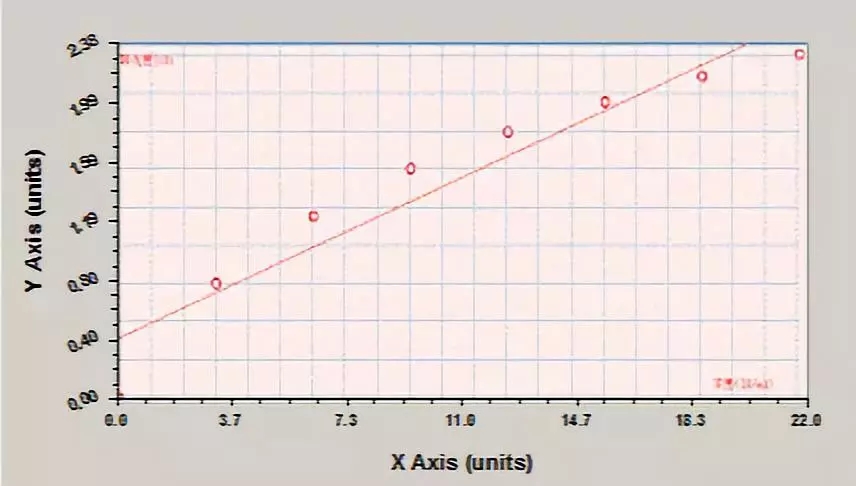
06 Logit-Log 拟合回归方程
Logit-log 则是免疫学检测中的模型, 可用于竞争法。它最早用于 RIA，但在 ELISA 中也是可以应用的。Logit 变换源于数学中的 Logistic 曲线。在竞争法放射免疫分析 (RIA) 及 ELISA 中，当竞争性反应物为 0 时结合率为 100%，如果某一浓度下结合率为 B，B=OD/OD(0)，在对B进行 Logit 变换：y=ln[B/(1-B)]，之后 y 与浓度的对数成线性关系，即：y = a + b lg(x)，拟合函数方程式为：lg(y) = a lg(x) + b 就得到了 Logit-log 直线回归模型，这个模型一般适用于竞争法的拟合，所以拟合时要求只有少有一个零浓度测试的 OD 值，并且此值为整个反应的最大值(也就是我们常说的至少要做一个空白对照)。

07 四参数拟合回归方程
四参数方程的拟合函数表达式为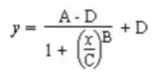：新闻图片6

竞争法和夹心法都可以用到。它的形状, 根据情况, 可能是一个单调上升的类似指数, 对数, 或双曲线的曲线, 也可能是一个单调下降的上述曲线, 还可以是一条 S 形曲线。它要求 X 值不能小于 0 (因为指数是实数, 故有此要求)。在很多情况下它都可以拟合 ELISA 的反应曲线, 所以它也成了 ELISA 中应用最广的模型之一。

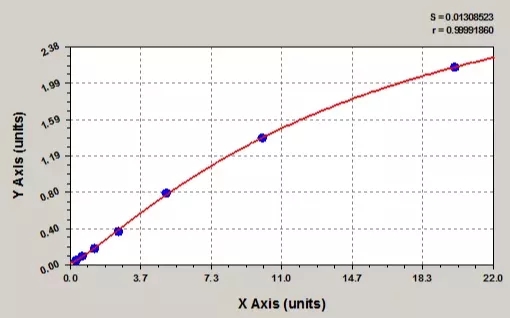
新闻图片7

切记，在实验过程中，要根据各个实验本身的特点，选择最适合的曲线拟合模型，才能得到最合理的实验结果, 一般情况下，需要综合考虑标准曲线的趋势走向以及 R 值的大小，来最终选择适合自己的回归方程。

Sirt1靶点检测详解

发文献，领奖励

更多资讯

我的询价

武汉菲恩生物科技有限公司品牌商